Zad. 1. Znajdź liczby naturalne dwucyfrowe, dla których liczba półtora raza większa jest również liczbą naturalną dwucyfrową i ma taką samą sumę cyfr.
Zad. 2. Wpisując w każdą kratkę kwadratu po jednej cyfrze różnej od zera, otrzymujemy cztery liczby dwucyfrowe: dwie poziome i dwie pionowe. Wpisz takie cyfry, aby suma tych czterech liczb była równa 67.

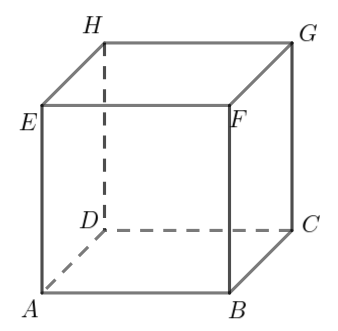
Zad. 3. Każda trójka wierzchołków sześcianu wyznacza pewien trójkąt. Ile wśród nich jest trójkątów prostokątnych?
W lutym punkty zdobyli:
• 3 –Maja Bator SP 44 Wrocław, Cezary Bogacz SP Krzeptów, Arseniia Elkina SP 16 Wrocław, Daria Karnitskaya SP 107 Wrocław, Zofia Lorenz SP 3 Mikołów, Oliwier Makuch SP 1 Szprotawa, Adam Trznadel SP 82 Wrocław;
• 2,5 – Sebastian Aksamit SP 16 Wrocław, Maria Bogner SP Fundacji Królowej św. Jadwigi Wrocław, Kajetan Bondarewicz SP 23 Wrocław, Marcel Borkowski SP Zbuczyn, Piotr Celiński SP Fundacji Królowej św. Jadwigi Wrocław, Jakub Ceynowa SP 95 Wrocław, Michał Filipczak SP 44 Wrocław, Zuzanna Fita SP 44 Wrocław, Anna Gil SP 44 Wrocław, Jakub Gil SP 44 Wrocław, Mateusz Jaszczyszyn SP 44 Wrocław, Filip Kaźmierczak SP 44 Wrocław, Marie Łobos SP "Młody Kopernik" Wałbrzych, Sophie Łobos SP "Młody Kopernik" Wałbrzych, Anastazja Marciniak SP 3 Mogilno, Mateusz Noga SP 113 Wrocław, Piotr Strzelecki SP 50 Wrocław, Michał Synakiewicz SP Brzoza, Aleksandra Wabińska SP Żerniki Wrocławskie, Zuzanna Winiarska SP 44 Wrocław;
• 2 – Filip Fudała SP 53 Wrocław, Zuzanna Głowacz SP Popielów, Zuzanna Głowacz SP Popielów, Kacper Jarzyński SP 13 Zielona Góra, Piotr Kostanek SP Mińsk Mazowiecki, Małgorzata Nowakowska SP 3 Głogów, Nina Pociecha SP 100 STO Warszawa, Natalia Rodziewicz SP Szczytno, Kalina Tułacz SP 50 Wrocław, Julian Wawer SP Pilawa;
• 1,5 – Wilhelm Bardowski SP 1 Lubań, Krzysztof Bednarz SP Głogów Małopolski, Nela Bielecka SP Żerniki Wrocławskie, Mieszko Buczkowski SP 2 Ożarów Mazowiecki, Tomasz Cichopek SP Świebodzice, Michał Derewecki SP 50 Wrocław, Gabriela Gajdzis SP 8 Zielona Góra, Antoni Gałkowski SP Józefów n. Wisłą, Wojciech Gdesz SP Żerniki Wrocławskie, Stanisław Góralski SP Józefów n. Wisłą, Lena Gębowska SP 50 Wrocław, Laura Kogut SP 9 Gliwice, Dominika Kubica SP "Płomień" Katowice, Alicja Lis SP 50 Wrocław, Antoni Łakomiec SP 50 Wrocław, Tobiasz Mazurkiewicz SP Popielów, Julian Pendziałek SP Popielów, Irmina Pietroń SP Józefów n. Wisłą, Leon Płonka SP 44 Wrocław, Amelia Prejs SP Józefów n. Wisłą, Zofia Romiszewska SP 100 STO Warszawa, Nina Roziel SP 50 Wrocław, Mateusz Różalski SP Józefów n. Wisłą, Anna Rudzińska SP 28 Warszawa, Wiktor Sędziak SP 28 Bielsko-Biała, Karol Sobecki SP 28 Bielsko-Biała, Franciszek Sobka SP Józefów n. Wisłą, Witold Stępień SP 1 Oleśnica, Dawid Szymala SP 50 Wrocław, Amelia Waindok SP 3 Dobrzeń Wielki, Michał Witkowski SP Przedmoście, Kacper Wołowiec SP 50 Wrocław, Krzysztof Wróblewski SP Bielkówko, Ignacy Żak SP Żerniki Wrocławskie;
• 1 – Jeremi Bablok SP Bednarska (Terytorium Mysłowicka) Warszawa, Maciej Budas SP Popielów, Luiza Gruchalski SP Dobrzeń Wielki, Kurt Kolodii SP 44 Wrocław, Julian Tomczak SP SP 16 Wrocław.
Pozostali uczestnicy otrzymali poniżej 1 punktu.
Zad. 1. Niech n będzie szukaną liczbą. Liczba 1,5 razy większa jest nadal dwucyfrowa, więc
1,5n ≤ 99, czyli n≤66. Skoro 1,5n jest naturalna, n musi być parzysta (dlaczego?). Ponadto
1,5n = 3/2 n jest podzielna przez 3 (dlaczego?), a skoro n ma tę samą sumę cyfr, także musi być podzielne przez 3 (na podstawie cechy podzielności przez 3). Stąd wynika, że n=6k, gdzie
k ∈ {2, 3, 4, …, 11}. Wówczas 1,5n = 9k, czyli 1,5n jest podzielna przez 9. Ale wtedy (na mocy cechy podzielności przez 9) liczba n też musi być podzielna przez 9. Liczb spełniających warunki zadania szukamy więc wśród parzystych wielokrotności liczby 9 nie większych niż 66. Są to liczby 18, 36 i 54.
Zad. 2. Są dwa możliwe rozwiązania, różniące się kierunkiem odczytywania liczb. W obu przypadkach mamy 11+12+17+27=67.
![]()
Zad. 3. Na wierzchołkach sześcianu można rozpiąć albo trójkąty prostokątne (np. ABF lub ACG), albo równoboczne (np. ACF - każdy bok jest przekątną kwadratu). Trójkątów równobocznych jest 8 (które to trójkąty?). Wystarczy obliczyć, ile jest wszystkich trójkątów o wierzchołkach A, B, C, D, E, F, G, H. Na początek zauważmy, że wśród wierzchołków sześcianu nie ma trzech punktów leżących na jednej prostej, czyli każdy wybór trzech wierzchołków daje trójkąt. Aby wybrać trójkę wierzchołków, pierwszy wybieramy na 8 sposobów, do tego drugi na 7, a trzeci na 6, czyli całość na 8·7·6 sposobów. Jednak wśród utworzonych w ten sposób nazw trójkątów są szóstki opisujące tę samą figurę (np. ACF, AFC, CAF, CFA, FAC i FCA). Zatem każdy trójkąt liczony jest w ten sposób sześciokrotnie. Wszystkich trójkątów jest więc 8·7=56, a trójkątów prostokątnych jest
56–8=48.



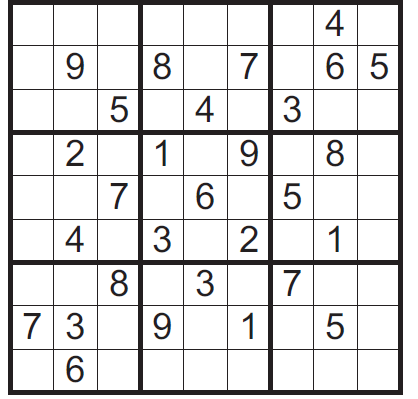
 To zabawny samouczek, który zaczynając się niewinnie intrygującą historyjką, krok po kroku, poczynając od najłatwiejszych łamigłówek, prowadzi nas w szpony, nie bójmy się użyć tego słowa, uzależnienia.
To zabawny samouczek, który zaczynając się niewinnie intrygującą historyjką, krok po kroku, poczynając od najłatwiejszych łamigłówek, prowadzi nas w szpony, nie bójmy się użyć tego słowa, uzależnienia.

Dobre
Dobre zadania w tym miesiącu.
Za co odjęte zostało 0,5 pkt. osobom, które dostały 2,5
Dzień dobry
Za co zostało odjęte 0,5 pkt osobom, które dostały 2,5 pkt i miały wszystkie odpowiedzi prawidłowe.