Zad. 1. W bębnie maszyny losującej znajduje się 20 kul z kolejnymi numerami od 1 do 20. Ile co najmniej kul trzeba wylosować, aby na pewno wśród wylosowanych:
a) były 2 kule o kolejnych numerach.
b) były 3 kule o kolejnych numerach.
c) były 4 kule o kolejnych numerach.
d) było 5 kul o kolejnych numerach.
Zad. 2. Kartkę papieru dzielimy na prostokąty za pomocą zaginania prostych poziomych i pionowych lub tylko pionowych (rysunek przedstawia przykładowy podział podział na 12 prostokątów przez zagięcie 5 prostych). Jaka liczba zagiętych prostych pozwoli uzyskać podział na:
a) 24 prostokąty?
b) 48 prostokątów?
c) 72 prostokąty?
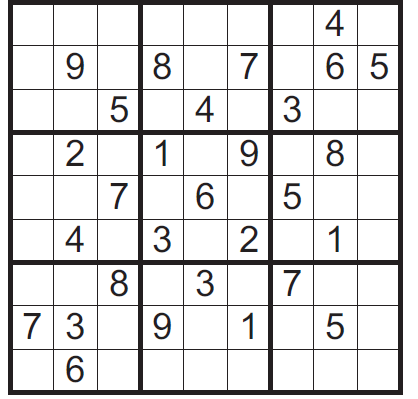
Zad. 3. Rozwiąż walentynkowe sudoku 6×6. W puste kratki wpisz użyte w diagramie litery tak, aby w każdym wierszu, kolumnie i pogrubionym prostokącie znajdowały się różne litery. W rozwiązaniu podaj ukryte w diagramie słowo oraz jego permutacje znajdujące się w II, III, IV i V wierszu.
W tym miesiącu punkty zdobyli:
- 3 - Daria Bumażnik - doktorantka na Wydziale Chemii UWr, Elżbieta Grzechnik - emerytowana nauvzycielka z Radomia, Dominika Horodecka - studentka WIMiO na Politechnice Gdańskiej, Vladislav Klyachin - programista z Berlina, Krystyna Lisiowska - redaktor z Warszawy, Oliwia Makuch - studentka Matematyki Stosowanej na PWr, Piotr Mazur - specjalista systemów ERP ze Złotoryi, Szymon Meyer - analityk danych z Dziewkowic, Olga Shut - programistka z Wrocławia, Marzena Wąsiewicz - nauczycielka z Kajetan, Michał Węgrzyn - student UWr,
- 2,5 - Cezary Rębiś - Zespół Szkół Elektronicznych Radom,
- 2 - Weronika Buchar - nauczycielka z Leszna, Agata Leśnicka - lekarz z Gdańska, Hanna Marcinowska III LO Opole, Wojciech Mura - student matematyki na UJ, Anna Niżałowska - LO Góra, Edward Nowicki- informatyk z Poznania, Kasper Przenzak - analityk ryzyka z Krakowa, Adam Stanisławski - programista z Wrocławia, Ignacy Włodarski SP 36 Wrocław.
Zad. 1. Kul trzeba wylosować co najmniej: a) 11, b) 15, c) 16, d)17.
Zad. 2. Aby uzyskać podział na k = n·m prostokątów, trzeba zagiąć (n–1)+(m–1) linii. Dla każdej liczby prostokątów należy rozważyć wszystkie możliwości.
a) 24 = 1·24 = 2·12 = 3·8 = 4·6, co daje liczby zagięć równe odpowiednio 23, 12, 9 i 8.
b) 48 = 1·48 = 2·24 = 3·16 = 4·12 = 6·8, co daje 47, 24, 17, 14 lub 12 zagięć.
c) 72 = 1·72 = 2·36 = 3·24 = 4·18 = 6·12 = 8·9, co daje 71, 36, 25, 20, 16 lub 15 zagięć.
Zad. 3. Ukryte słowo (niewystępujące w diagramie) to KOCHAJ. Szukane permutacje to: HAOJKC, OHCKJA, JKACOH, ACJOHK.
To zabawny samouczek, który zaczynając się niewinnie intrygującą historyjką, krok po kroku, poczynając od najłatwiejszych łamigłówek, prowadzi nas w szpony, nie bójmy się użyć tego słowa, uzależnienia.
